Link
Highlights&&Note
feature在CNN中也被成为卷积核(filter),一般是3X3,或者5X5的大小
^3ecb3c65卷积神经网络在本质和原理上还是和卷积运算有一定的联系的
^e3448be7好了,经过一系列卷积对应相乘,求均值运算后,我们终于把一张完整的feature map填满了。
^3775cc34非线性激活层
卷积层对原图运算多个卷积产生一组线性激活响应,而非线性激活层是对之前的结果进行一个非线性的激活响应。
指的是对卷积得到的结果再次处理.
非线性激活使用的就是非线性激活函数 ^a7676697
卷积操作后,我们得到了一张张有着不同值的feature map,尽管数据量比原图少了很多,但还是过于庞大(比较深度学习动不动就几十万张训练图片),因此接下来的池化操作就可以发挥作用了,它最大的目标就是减少数据量。
池化分为两种,Max Pooling 最大池化、Average Pooling平均池化。顾名思义,最大池化就是取最大值,平均池化就是取平均值。
^251b2749
拿最大池化举例:选择池化尺寸为2x2,因为选定一个2x2的窗口,在其内选出最大值更新进新的feature map。
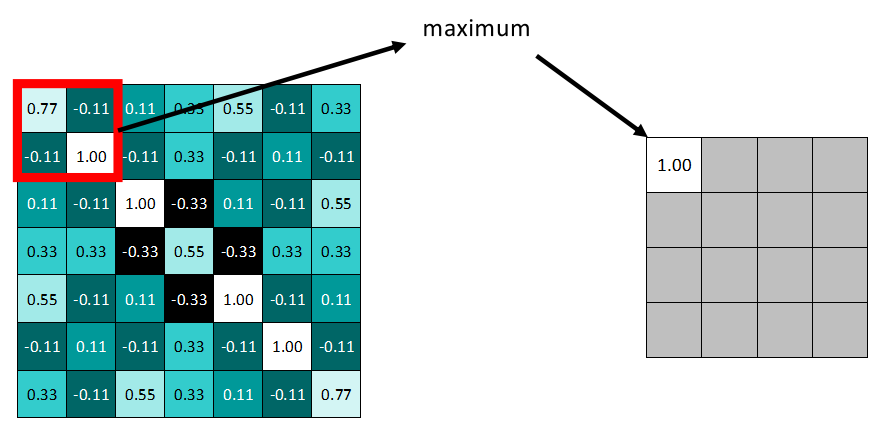
同样向右依据步长滑动窗口。
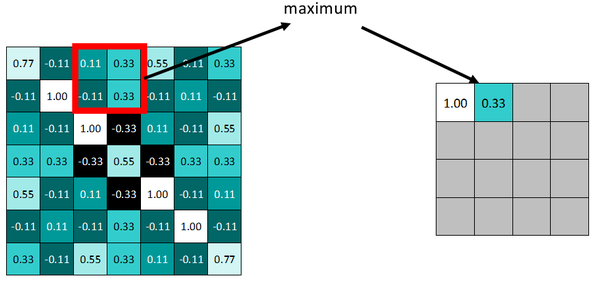
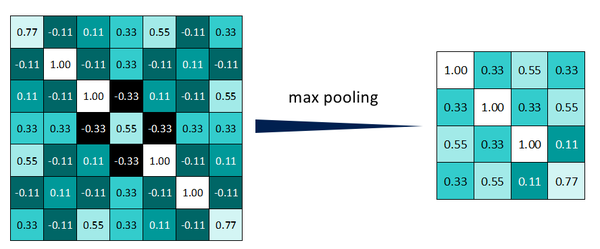
最终得到池化后的feature map。可明显发现数据量减少了很多。
^14292521
在常见的几种CNN中,这三层都是可以堆叠使用的,将前一层的输入作为后一层的输出。比如:
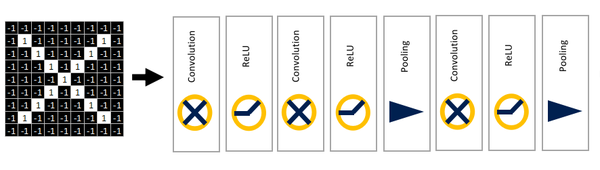
卷积,激活,池化三大层可以一直叠加欸 ^11d0531b
Content
目录导读
【1】导论
【2】卷积运算
【3】非线性激活
【4】池化层
【5】全连接层
【6】神经网络的训练与优化
【7】想到再补充
【1】导论
先来说一写题外话…
研究生入学后就被导师逼着学习神经网络,一开始非常盲目,先是在网上搜了一大堆的资料,各种什么“一文读懂卷积神经纹网络”,“叫你三分钟搭建属于自己的神经网络框架”,“五分钟速读神经网络全解”,之类的文章层出不穷。看了太多导致的结果是,学了很久都没能真正意义上地入门。
而后自己艰辛摸索才慢慢了解了卷积神经网络的真谛。(好官方啊哈哈哈哈哈哈)
首先最需要明确的一点就是,卷积神经网络,也就是convolutional neural networks (简称CNN),现在已经被用来应用于各个领域,物体分割啦,风格转换啦,自动上色啦blahblah,但是!!CNN真正能做的,只是起到一个特征提取器的作用!所以这些应用,都是建立在CNN对图像进行特征提取的基础上进行的。
这篇文章呢,我不打算和传统介绍CNN的文章一样先介绍生物神经元、突触什么的,就直接从最简单的实例讲起。
废话不多说,开始。
拿到一张图片,要对它进行识别,最简单的栗子是,这张图是什么?
比如,我现在要训练一个最简单的CNN,用来识别一张图片里的字母是X还是O。

我们人眼一看,很简单嘛,明显就是X啊,但是计算机不知道,它不明白什么是X。所以我们给这张图片加一个标签,也就是俗称的Label,Label=X,就告诉了计算机这张图代表的是X。它就记住了X的长相。
但是并不是所有的X都长这样呀。比如说…

这四个都是X,但它们和之前那张X明显不一样,计算机没见过它们,又都不认识了。
(这里可以扯出机器学习中听起来很高冷的名词 “ 欠拟合 ”)
不认识了怎么办,当然是回忆看看是不是见过差不多的呀。这时候CNN要做的,就是如何提取内容为X的图片的特征。
我们都知道,图片在计算机内部以像素值的方式被存储,也就是说两张X在计算机看来,其实是这样子的。


其中1代表白色,-1代表黑色。
如果按照每像素逐个比较肯定是不科学的,结果不对而且效率低下,因此提出其他匹配方法。
我们称之为patch匹配。
观察这两张X图,可以发现尽管像素值无法一一对应,但也存在着某些共同点。
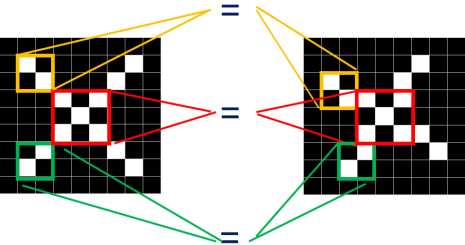
如上图所示,两张图中三个同色区域的结构完全一致!
因此,我们就考虑,要将这两张图联系起来,无法进行全体像素对应,但是否能进行局部地匹配?
答案当然是肯定的。
相当于如果我要在一张照片中进行人脸定位,但是CNN不知道什么是人脸,我就告诉它:人脸上有三个特征,眼睛鼻子嘴巴是什么样,再告诉它这三个长啥样,只要CNN去搜索整张图,找到了这三个特征在的地方就定位到了人脸。
同理,从标准的X图中我们提取出三个特征(feature)
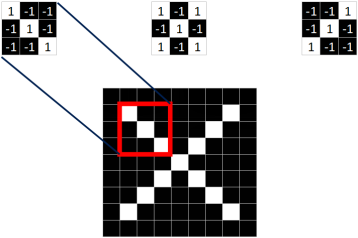
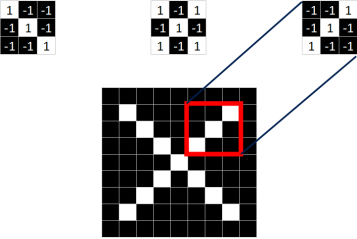
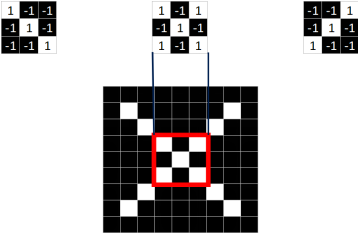
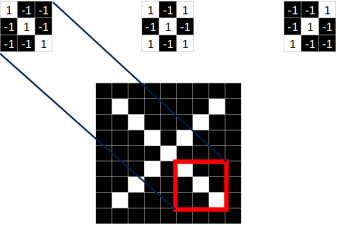
我们发现只要用这三个feature便可定位到X的某个局部。
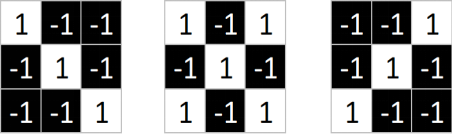
==feature在CNN中也被成为卷积核(filter),一般是3X3,或者5X5的大小==。
【2】卷积运算
说了那么久终于扯到了卷积二字!
但是!!胖友们!卷积神经网络和信号处理里面那个卷积运算!毛关系都没有啊!当初我还特意去复习了一下高数里的卷积运算!摔!
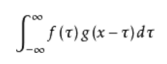
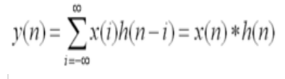
这些!!都和我们的CNN没有关系!!!
(二稿修改:经知友提醒,此处的确说的不对,==卷积神经网络在本质和原理上还是和卷积运算有一定的联系的==,只是之前本人才疏学浅未能看出它们二者实质相关联的地方,若有误导之处还请各位谅解,抱歉!)
好了,下面继续讲怎么计算。四个字:对应相乘。
看下图。
取 feature里的(1,1)元素值,再取图像上蓝色框内的(1,1)元素值,二者相乘等于1。把这个结果1填入新的图中。
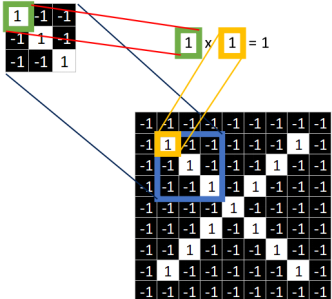
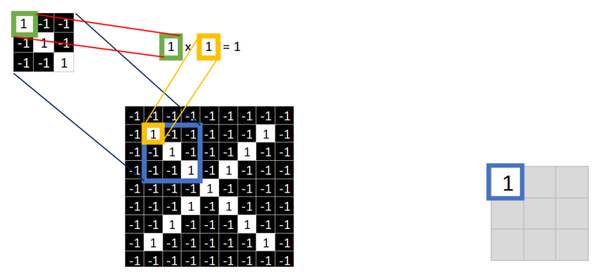
同理再继续计算其他8个坐标处的值
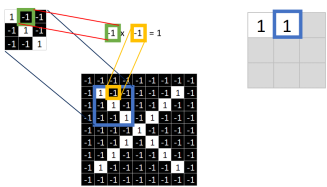
9个都计算完了就会变成这样。
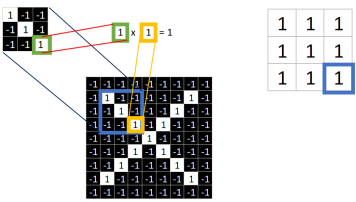
接下来的工作是对右图九个值求平均,得到一个均值,将均值填入一张新的图中。
这张新的图我们称之为 feature map (特征图)
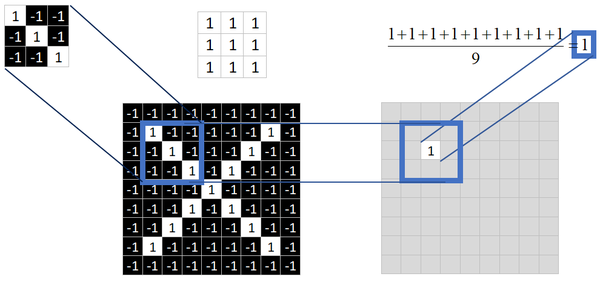
可能有小盆友要举手问了,为什么蓝色框要放在图中这个位置呢?
这只是个栗子嘛。 这个蓝色框我们称之为 “窗口”,窗口的特性呢,就是要会滑动。
其实最开始,它应该在起始位置。

进行卷积对应相乘运算并求得均值后,滑动窗便开始向右边滑动。根据步长的不同选择滑动幅度。
比如,若 步长 stride=1,就往右平移一个像素。

若 步长 stride=2,就往右平移两个像素。

就这么移动到最右边后,返回左边,开始第二排。同样,若步长stride=1,向下平移一个像素;stride=2则向下平移2个像素。

==好了,经过一系列卷积对应相乘,求均值运算后,我们终于把一张完整的feature map填满了。==
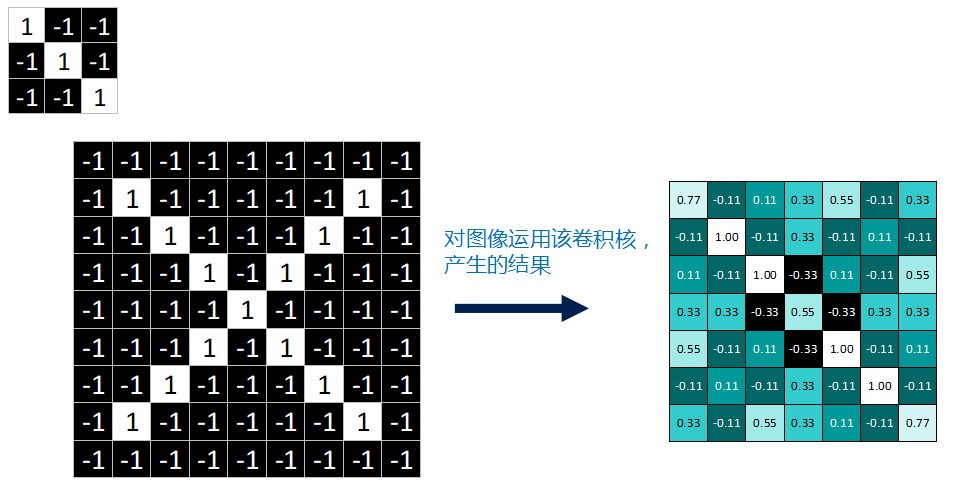
feature map是每一个feature从原始图像中提取出来的“特征”。其中的值,越接近为1表示对应位置和feature的匹配越完整,越是接近-1,表示对应位置和feature的反面匹配越完整,而值接近0的表示对应位置没有任何匹配或者说没有什么关联。
一个feature作用于图片产生一张feature map,对这张X图来说,我们用的是3个feature,因此最终产生3个 feature map。

至此,卷积运算的部分就讲完啦!~
【3】==非线性激活层==
==卷积层对原图运算多个卷积产生一组线性激活响应,而非线性激活层是对之前的结果进行一个非线性的激活响应。==
这是一个很官方的说法,不知道大家看到上面这句话是不是都觉得要看晕了。
嗯~ o(* ̄▽ ̄*)o 其实真的没有那么复杂啦!
本系列的文章秉承着“说人话!”的原则,着力于用最简单通俗的语言来为大家解释书上那些看不懂的概念。
在神经网络中用到最多的非线性激活函数是Relu函数,它的公式定义如下:
f(x)=max(0,x)
即,保留大于等于0的值,其余所有小于0的数值直接改写为0。
为什么要这么做呢?上面说到,卷积后产生的特征图中的值,越靠近1表示与该特征越关联,越靠近-1表示越不关联,而我们进行特征提取时,为了使得数据更少,操作更方便,就直接舍弃掉那些不相关联的数据。
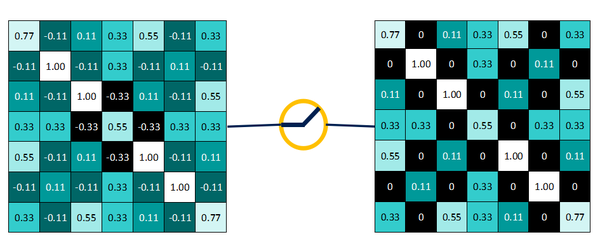
如下图所示:>=0的值不变
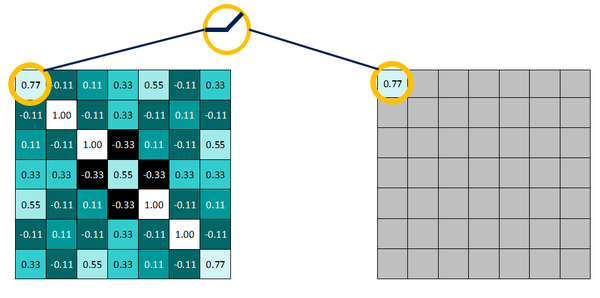
而<0的值一律改写为0
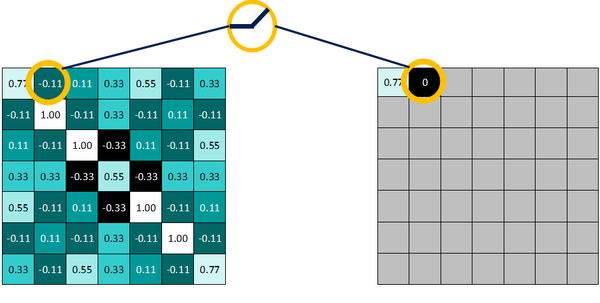
得到非线性激活函数作用后 的结果:
【4】pooling池化层
==卷积操作后,我们得到了一张张有着不同值的feature map,尽管数据量比原图少了很多,但还是过于庞大(比较深度学习动不动就几十万张训练图片),因此接下来的池化操作就可以发挥作用了,它最大的目标就是减少数据量。==
==池化分为两种,Max Pooling 最大池化、Average Pooling平均池化。顾名思义,最大池化就是取最大值,平均池化就是取平均值。==
==拿最大池化举例:选择池化尺寸为2x2,因为选定一个2x2的窗口,在其内选出最大值更新进新的feature map。==

==同样向右依据步长滑动窗口。==


==最终得到池化后的feature map。可明显发现数据量减少了很多。==
因为最大池化保留了每一个小块内的最大值,所以它相当于保留了这一块最佳匹配结果(因为值越接近1表示匹配越好)。这也就意味着它不会具体关注窗口内到底是哪一个地方匹配了,而只关注是不是有某个地方匹配上了。这也就能够看出,CNN能够发现图像中是否具有某种特征,而不用在意到底在哪里具有这种特征。这也就能够帮助解决之前提到的计算机逐一像素匹配的死板做法。
到这里就介绍了CNN的基本配置—-卷积层、Relu层、池化层。
==在常见的几种CNN中,这三层都是可以堆叠使用的,将前一层的输入作为后一层的输出。比如:==

也可以自行添加更多的层以实现更为复杂的神经网络。
而最后的全连接层、神经网络的训练与优化,更多内容将在下一篇文章中继续。
(文章更新多说几句:
感谢大家的赞与评论,我本来只是打算为自己的深度学习之路做一个记录,没想到真的有人在认真看这篇文章,很开心自己写的东西能被大家喜欢。
也很遗憾我只是一个还在继续学习中的学生,因此无法做到全面讲述到位,只是为和曾经的我一样为入门而苦恼的初学者提供另一种学习思路,这篇文章很是浅显,若是读者朋友有什么意见与批评,欢迎在评论栏里一起讨论!谢谢)